Irrational winding of a torus
In topology, a branch of mathematics, irrational winding of a torus is a continuous injection of a line into a torus that is used to set up several counterexamples.[1] A related notion is Kronecker foliation.
Contents |
Definition
Consider a torus  , and the corresponding projection
, and the corresponding projection  . The points of the torus correspond to (translated) points of a square lattice in
. The points of the torus correspond to (translated) points of a square lattice in 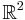 that is
that is  , and
, and  factors through a map that takes any point to a point in
factors through a map that takes any point to a point in  given by the fractional parts of the original point's standard coordinates. Now consider a line in
given by the fractional parts of the original point's standard coordinates. Now consider a line in 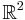 given by the equation y = kx. If k is rational, then it can be represented by a fraction and a corresponding lattice point of
given by the equation y = kx. If k is rational, then it can be represented by a fraction and a corresponding lattice point of  . It can be shown that then the projection of this line is a simple closed curve on a torus. If, however, k is irrational, then it will not cross any lattice points except 0, which means that its projection on the torus will not be a closed curve, and the restriction of
. It can be shown that then the projection of this line is a simple closed curve on a torus. If, however, k is irrational, then it will not cross any lattice points except 0, which means that its projection on the torus will not be a closed curve, and the restriction of  on this line is injective. Moreover, it can be shown that the image of this restricted projection as a subspace, called the irrational winding of a torus, is dense in the torus.
on this line is injective. Moreover, it can be shown that the image of this restricted projection as a subspace, called the irrational winding of a torus, is dense in the torus.
Applications
Irrational winding of a torus is used to set up a few counter-examples related to monomorphisms. It is an immersed submanifold but not a regular submanifold of the torus, which shows that the image of a manifold under a continuous injection to another manifold is not necessarily a (regular) submanifold.[2] It is also an example of the fact that the induced submanifold topology does not have to coincide with the subspace topology of the submanifold [2] a[›]
Secondly, the torus can be considered as a Lie group 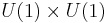 , and the line can be considered as
, and the line can be considered as  . Then it is easy to show that the image of the continuous and analytic group homomorphism
. Then it is easy to show that the image of the continuous and analytic group homomorphism  is not a Lie subgroup[2][3] (because it's not closed in the torus) while, of course, it is still a group. It is also used to show that if a subgroup H of the Lie group G is not closed, the quotient G/H does not need to be a submanifold[4] and even not a Hausdorff space.
is not a Lie subgroup[2][3] (because it's not closed in the torus) while, of course, it is still a group. It is also used to show that if a subgroup H of the Lie group G is not closed, the quotient G/H does not need to be a submanifold[4] and even not a Hausdorff space.
See also
Notes
^ a: As a topological subspace of the torus, the irrational winding is not a manifold at all, because it is not locally homeomorphic to  .
.
References
- ^ D. P. Zhelobenko. Compact Lie groups and their representations. http://books.google.com/books?id=ILhUYVmvHt0C&pg=PA45.
- ^ a b c Loring W. Tu (2010). An Introduction to Manifolds. Springer. pp. 168. ISBN 978-1441973993.
- ^ Čap, Andreas; Slovák, Jan (2009), Parabolic Geometries: Background and general theory, AMS, pp. 24, ISBN 978-0821826812, http://books.google.com/books/about/Parabolic_Geometries_Background_and_gene.html?id=G4Ot397nWsQC
- ^ Sharpe, R.W. (1997), Differential Geometry: Cartan's Generalization of Klein's Erlangen Program, Springer-Verlag, New York, pp. 146, ISBN 0-387-94732-9